Introduction to Sound Frequencies in Music
Music is an art form deeply rooted in science, particularly in the physics of sound. Every musical note you hear corresponds to a specific frequency, measured in Hertz (Hz), which determines its pitch. Understanding these frequencies is essential for musicians, producers, and audio engineers, as it helps with tuning instruments, composing music, and sound design.
Sound frequencies are vibrations that travel through the air, creating waves that our ears perceive as pitch. The faster the vibration, the higher the pitch, and vice versa. In Western music, the standard tuning system is based on A4 (the A above middle C) set at 440 Hz, though some orchestras and genres use slight variations like 432 Hz or 442 Hz.
This guide will break down the frequencies of musical notes, explain how octaves influence pitch, and explore practical applications for musicians.
Easily convert frequency in Hz to musical notes, MIDI numbers, and pitch in cents. Use this fast, accurate online frequency-to-note converter tool, ideal for musicians, producers, and audio engineers.
Breakdown of Note Frequencies (C, D, E, F, G, A, B)
In Western music, the chromatic scale consists of 12 notes, each separated by a semitone (half step). The seven natural notes—C, D, E, F, G, A, B—are the white keys on a piano, while the remaining five (sharps/flats) are the black keys.
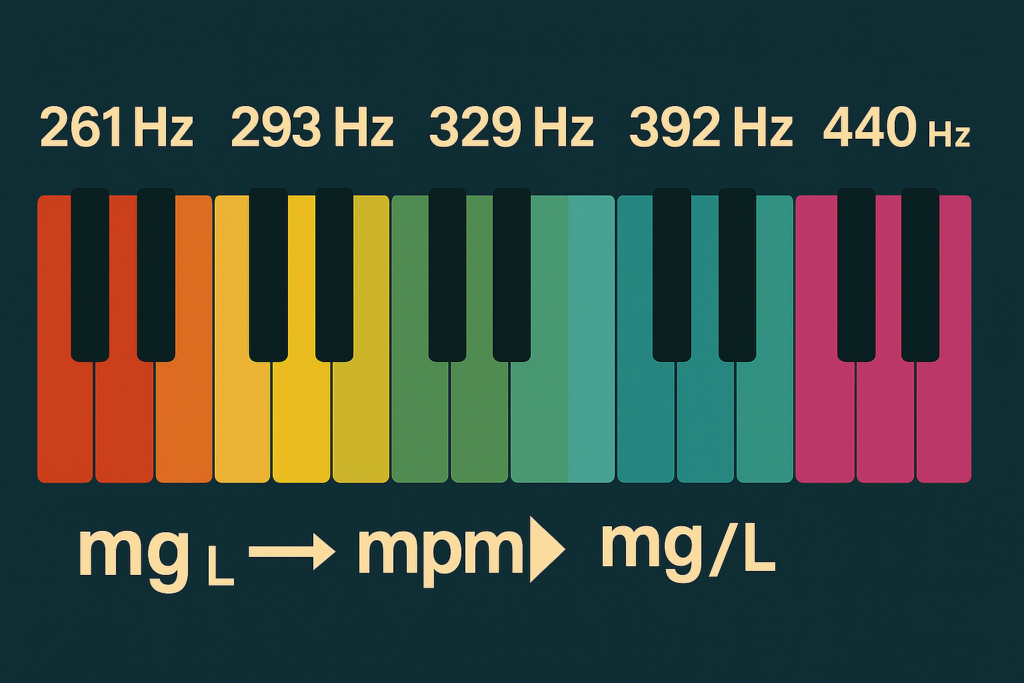
Here are the frequencies of the natural notes in the 4th octave (C4 to B4), based on A4 = 440 Hz tuning:
- C4 (Middle C): 261.63 Hz
- D4: 293.66 Hz
- E4: 329.63 Hz
- F4: 349.23 Hz
- G4: 392.00 Hz
- A4: 440.00 Hz (standard tuning reference)
- B4: 493.88 Hz
Each note’s frequency is calculated using the formula:
[ f(n) = 440 \times 2^{(n-49)/12} ]
Where:
- ( f(n) ) = frequency of the nth note
- ( n ) = the key number on a piano (A4 is key 49)
This formula ensures that each semitone increases the frequency by a factor of ( 2^{1/12} ) (about 1.05946), maintaining equal temperament tuning.
How Octaves Affect Frequency (C4 vs. C5)
An octave is the interval between one musical pitch and another with double (or half) its frequency. For example:
- C4 (Middle C): 261.63 Hz
- C5 (next higher C): 523.25 Hz (exactly double C4)
- C3 (lower octave): 130.81 Hz (half of C4)
This doubling effect means that every octave shift either multiplies or divides the frequency by 2. This principle applies to all notes, not just C.
Why Octaves Sound Similar to Our Ears
Despite the frequency difference, notes separated by an octave sound harmonically related because they share the same “tonal quality.” This phenomenon is due to the way our brains process sound waves—frequencies that are powers of two apart reinforce each other harmonically.
Practical Applications for Musicians
Understanding note frequencies is crucial for various musical applications:
1. Tuning Instruments
- Musicians use tuners to match their instruments to standard frequencies (e.g., A4 = 440 Hz).
- Guitarists adjust string tension to hit precise frequencies for each note.
2. Music Production & Sound Design
- Producers use frequency charts to EQ instruments properly (e.g., cutting muddiness around 200-300 Hz).
- Synthesizers generate tones by manipulating waveforms at specific frequencies.
3. Harmony & Chord Construction
- Notes with simple frequency ratios (e.g., 3:2 for a perfect fifth) sound consonant.
- Understanding frequencies helps in tuning intervals for perfect harmony.
4. Instrument Building & Repair
- Piano tuners adjust string tension based on frequency calculations.
- Wind instrument makers design bore lengths to resonate at desired pitches.
5. Alternative Tuning Systems
- Some musicians experiment with different tuning standards (e.g., A = 432 Hz for a “softer” sound).
- Microtonal music uses frequencies outside the standard 12-tone system.
Frequency Charts for Quick Reference
For easy access, here’s a frequency chart for notes across multiple octaves (based on A4 = 440 Hz):
| Note | Octave 3 (Hz) | Octave 4 (Hz) | Octave 5 (Hz) |
|---|---|---|---|
| C | 130.81 | 261.63 | 523.25 |
| D | 146.83 | 293.66 | 587.33 |
| E | 164.81 | 329.63 | 659.26 |
| F | 174.61 | 349.23 | 698.46 |
| G | 196.00 | 392.00 | 784.00 |
| A | 220.00 | 440.00 | 880.00 |
| B | 246.94 | 493.88 | 987.77 |
How to Use the Chart:
- Pianists: Locate notes by octave number (e.g., C4 is Middle C).
- Guitarists: Match fretted notes to frequencies (e.g., the 5th fret on the E string is A4 = 440 Hz).
- Producers: Use frequencies to identify pitch ranges in mixing (e.g., basslines typically sit between 40-200 Hz).
Conclusion
Musical note frequencies are the foundation of pitch, harmony, and tuning in music. By understanding how frequencies work, musicians can improve their tuning accuracy, enhance their compositions, and explore creative sound design. Whether you’re a performer, producer, or instrument maker, mastering these concepts will deepen your appreciation of music’s scientific beauty.
Keep this guide handy as a reference, and experiment with frequencies to discover new sonic possibilities in your musical journey!